2017
MATHEMATICS
Compulsory
Time: Three Hours and Fifteen Minutes
Full Marks {90 – For Regular Candidates, 100 For External Candidate}
1. নিম্নলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তরটি নির্বাচন করঃ (1×6=6)
(i) কোনো আসল ও তার বার্ষিক সবৃদ্ধি মূলের অনুপাত 25:28 হলে বার্ষিক সুদের হার –
(a) 3%
(b) 12%
(c) 10 পূর্ণ 5/7 %
(d) 8%
(ii) কোন শর্তে ax2+bx+c =0 দ্বিঘাত সমীকরণের একটি বীজ শূন্য হবে ?
(a)a=0
(b) b=0
(c) c = 0
(d) কোনোটিই নয়
(iii) দুটি বৃত্ত পরস্পরকে ছেদ বা স্পর্শ না করলে বৃত্ত দুটির সাধারণ স্পর্শকের সংখ্যা –
(a) 2 টি
(b) 1 টি
(c) 3 টি
(d) 4 টি
(iv) sinϴ= cosϴ হলে 2ϴ -এর মান হবে –
(a) 30°
(b) 60°
(c) 45°
(d) 90°
(v) একটি শঙ্কুর ভূমির ব্যাসার্ধের দৈর্ঘ্য এবং উচ্চতা প্রত্যেকটি দ্বিগুন হলে , শঙ্কুটির আয়তন হয় পূর্বের শঙ্কুর আয়তনের –
(a) 3 গুন
(b) 4 গুন
(c) 6 গুন
(d) 8 গুন।
(vi) 2, 8, 2, 3, 8, 5, 9, 5, 6 সংখ্যাগুলির মধ্যমা –
(a) 8
(b) 6.5
(c) 5.5
(d) 5
2. শূন্যস্থান পূরণ করঃ (যে কোনো পাঁচটি) । (1×5=5)
(i) কোনো মূলধনের বার্ষিক শতকরা একই সুদের হারে _________ বছরের সরল সুদ ও চক্রবৃদ্ধি সুদের পরিমাণ সমান ।
Ans: এক।
(ii) ax2+bx+c =0(a¹0) দ্বিঘাত সমীকরণের b2 -4ac হলে বীজদ্বয় বাস্তব ও _________হবে ।
Ans: সমান।
(iii) দুটি ত্রিভুজের বাহুগুলির দৈর্ঘ্যের পরিমাপ সমানুপাতে থাকলে ত্রিভুজ দুটি ___________ হবে ।
Ans: সদৃশ।
(iv) cos2ϴ-sin2ϴ= 1/X হলে , cos4ϴ -sin4ϴ= __________
Ans: 1/X
(v) একটি নিরেট অর্ধ- গোলোকের সমতল সংখ্যা _________ ।
Ans: একটি ।
(vi) x1, x2, x3, ………, xn এই n সংখ্যক সংখ্যার গড় x̅ হলে, Kx1, Kx2, Kx3, ……. Kxn এর গড় __________ ।
Ans: k x̅
3. সত্য বা মিথ্যা লেখো (যে কোনো পাঁচটি): (1×5=5)
(i) A 10000 টাকা দিয়ে ব্যাবসা শুরু করার 6 মাস পরে B 20000 টাকা দিল । বৎসরান্তে তাদের লভ্যাংশের পরিমাণ সমান হবে ।
Ans: সত্য।
(ii) x = 2+√3 হলে, x + 1/x এর মান হবে 2√3
Ans: মিথ্যা।
(iii) 7 সেমি. ও 3 সেমি. ব্যাসার্ধ বিশিষ্ট দুটি বৃত্ত বহিঃস্পর্শ করলে তাদের কেন্দ্র দ্বয়ের মধ্যে দূরত্ব 4 সেমি. হবে ।
Ans: মিথ্যা।
(iv) 0° < ϴ< 90° হলে, sinϴ> sin2ϴ হবে ।
Ans: সত্য।
(v) একটি অর্ধগোলোকের সমগ্রতলের ক্ষেত্রফল 36π বর্গ সেমি হলে উহার ব্যাসার্ধ 3 সেমি. হবে ।
Ans: মিথ্যা।
(vi) ওজাইভ দুটির ছেদবিন্দু থেকে x অক্ষের উপর লম্ব টানলে , x অক্ষ ও লম্বের ছেদবিন্দুর ভুজই হল মধ্যমা ।
Ans: সত্য।
4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাও (যে কোনো দশটি): (2×10=20)
(i) r% হার চক্রবৃদ্ধি সুদে কোনো মূলধন 8 বছরে দ্বিগুন হলে কত বছরে 4 গুন হবে?
(ii) কোনো এক ব্যাবসায় A এর মূলধন B এর মূলধনের দেড়গুণ । ওই ব্যাবসায় বৎসরান্তে B 1500 টাকা লভ্যাংশ পেলে, A কত টাকা লভ্যাংশ পাবে ?
(iii) সমাধান না করে p এর যে সকল মানের জন্য x2 +(p-3)x+p=0 সমীকরণের বাস্তব ও সমান বীজ আছে তা নির্ণয় কর ।
(iv) x ∝ yz এবং y ∝zx হলে , দেখাও যে , z (≠0) একটি ধ্রুবক ।
(v) দুটি সদৃশকোণী ত্রিভুজের পরিসীমা যথাক্রমে 20 সেমি. ও 16 সেমি. । প্রথম ত্রিভুজের একটি বাহুর দৈর্ঘ্য 9 সেমি. হলে দ্বিতীয় ত্রিভুজের অনুরূপ বাহুর দৈর্ঘ্য কত ?
(vi) ∆ABC এর ∠ABC =90°, AB =5সেমি, BC=12 সেমি. হলে ওই ত্রিভুজটির পরিব্যাসার্ধ কত ?
(vii) ABC ত্রিভুজের AB=(2a-1) সেমি, AC= 2√(2a) সেমি. এবং BC=(2a+1) সেমি. হলে, ∠BAC এর মান কত ?
(viii) x = asecϴ, y = btanϴ হলে, x ও y এর ϴ বর্জিত সম্পর্ক নির্ণয় কর ।
(ix) tan(ϴ+15°) = √3, হলে, sinϴ+cosϴ এর মান হিসাব করে লিখি ।
(x) একটি গোলোকের ব্যাস অপর গোলোকের ব্যাসের দ্বিগুন । যদি বড় গোলোকটির সমগ্রতলের ক্ষেত্রফলের সংখ্যামান ছোট গোলোকটির আয়তনের সংখ্যামানের সমান হয় , তবে ছোট গোলোকটির ব্যাসার্ধ কত ?
(xi) একটি আয়তঘনকের তলসংখ্যা x, ধার সংখ্যা y, শীর্ষবিন্দুর সংখ্যা z এবং কর্ণের সংখ্যা p হলে, x-y+z+p – এর মান কত ?
(xii) যদি 11 ,12,14, x-2, x+4, x+9,32,38,47 রাশিগুলির ঊর্ধ্বক্রমানুসারে সাজানো এবং তাদের মধ্যমা 24 হলে, x এর মান নির্ণয় কর ।
5. যে কোনো একটি প্রশ্নের উত্তর দাও: (5×1=5)
(i) বার্ষিক 4% হার সুদে কত টাকার 2 বছরের সরল সুদ ও চক্রবৃদ্ধি সুদের অন্তর 80 টাকা হবে ।
(ii) A, B, C যৌথ ভাবে 1,80,000 টাকা দিয়ে একটি ব্যাবসা শুরু করল । A, B এর থেকে 20000 টাকা বেশী দিল । লাভের পরিমাণ 10800 টাকা ত্যাদের মধ্যে ভাগ করে দাও ।
6. যে কোনো একটি সমাধান কর: (3×1=3)
(ii) একটি ধনাত্মক অখণ্ড সংখ্যার পাঁচগুন,তার বর্গের দ্বিগুন অপেক্ষা 3 কম হলে সংখ্যাটি কত ?
7. যে কোনো একটি প্রশ্নের উত্তর দাও: (3×1=3)
(i) সরল করঃ
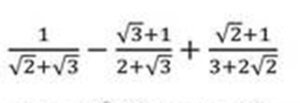
(ii) একটি হোস্টেলের ব্যায় আংশিক ধ্রুবক ও আংশিক ওই হোস্টেলের আবাসিকদের সংখ্যার সঙ্গে সরলভেদে আছে । আবাসিকদের সংখ্যা 120 হলে ব্যায় 2000 টাকা এবং আবাসিকদের সংখ্যা 100 হলে ব্যায় 1700 টাকা হয় । ব্যায় 1880 টাকা হলে হোস্টেলের আবাসিকদের সংখ্যা কত হবে ?
8. যে কোনো একটি প্রশ্নের উত্তর দাও: (3×1=3)
![]()
![]()
9. যে কোনো একটি প্রশ্নের উত্তর দাও: (5×1=5)
(i) যেকোনো ত্রিভুজের একটি বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান হলে প্রমাণ কর যে প্রথম বাহুর বিপরীত কোণটি সমকোণ হবে ।
(ii) কোনো বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে যে দুটি স্পর্শক অঙ্কন করা যায় তাদের স্পর্শবিন্দু দুটির সঙ্গে সংযোজক সরলরেখাংশ দুটির দৈর্ঘ্য সমান।
10. যে কোনো একটি প্রশ্নের উত্তর দাও: (3×1=3)
(i) প্রমাণ করো যে, কোনো চতুর্ভুজের কোণ চারটির সমদ্বিখণ্ডক গুলি পরস্পর মিলিত হয়ে যে চতুর্ভুজ গঠন করে, সেটি বৃত্তস্থ চতুর্ভুজ ।
(ii) ত্রিভুজ ABC এর পরিকেন্দ্র O এবং OD ⊥ BC, প্রমাণ কর যে ∠BOD =∠BAC ।
11. যে কোনো একটি প্রশ্নের উত্তর দাও: (5×1=5)
(i) 6 সেমি. বাহুবিশিষ্ট একটি সমবাহু ত্রিভুজ অঙ্কন করো এবং ওই ত্রিভুজটির অন্তবৃত্ত অঙ্কন করো । (কেবলমাত্র অঙ্কন চিহ্ন দিতে হবে )
(ii) 8 সেমি. ও 6 সেমি. বাহুবিশিষ্ট একটি আয়তক্ষেত্র অঙ্কন করো এবং ওই আয়তক্ষেত্রের সমান ক্ষেত্রফল বিশিষ্ট একটি বর্গক্ষেত্র অঙ্কন করো । (কেবলমাত্র অঙ্কন চিহ্ন দিতে হবে
12. যে কোনো দুটি প্রশ্নের উত্তর দাও: (4×2=8)
(i)কোনো চতুর্ভুজের তিনটি কোণের পরিমাপ যথাক্রমে π/3, 5π/6, 90° হলে, চতুর্থ কোণটির ষষ্টিক ও বৃত্তীয় মান হিসাব করে লিখি।
13. যে কোনো একটি প্রশ্নের উত্তর দাও: (5×1=5)
(i) দুটি স্তম্ভের দূরত্ব 150 মিটার । একটির উচ্চতা অন্যটির তিনগুন । স্তম্ভদ্বয়ের পাদদেশ সংযোগকারী রেখাংশের মধ্যবিন্দু থেকে তাদের শীর্ষের উন্নতি কোণদ্বয় পরস্পর পূরক । ছোট স্তম্ভটির উচ্চতা নির্ণয় কর ।
(ii) 10. একটি লাইট হাউস থেকে তার সঙ্গে একই সরলরেখায় অবস্থিত দুটি জাহাজের মাস্তুলের গোড়ার অবনতি কোণ যথাক্রমে 60° ও 30° হয় এবং কাছের জাহাজের মাস্তুল যদি লাইট হাউস থেকে 150 মিটারদুরত্বে থাকে, তাহলে দূরের জাহাজের মাস্তুল লাইট হাউস থেকে কত দূরত্বে রয়েছে ?
14. যে কোনো দুটি প্রশ্নের উত্তর দাও: (4×2=8)
(i) 4.2 ডেসিমি. দৈর্ঘ্যের ধারবিশিষ্ট একটি নিরেট ঘনক থেকে সবচেয়ে কম কাঠ নষ্ট করে যে নিরেট লম্ব বৃত্তাকার শঙ্কু পাওয়া যাবে তার আয়তন নির্ণয় করি ।
(ii) 9 সেমি. অন্তর্ব্যাসার্ধ বিশিষ্ট একটি অর্ধ গোলাকার পাত্র সম্পূর্ণ জলপূর্ণ আছে । এই জল 3 সেমি. ব্যাস এবং 4 সেমি. উচ্চতা বিশিষ্ট চোঙাকৃতি বোতলে ভর্তি করে রাখা হবে । পাত্রটি খালি করতে কতগুলি এইরূপ বোতল দরকার তা নির্ণয় কর ।
(iii) একটি ঢাকনা সমেত চোঙাকৃতি জলের ট্যাঙ্কের ভূমির ক্ষেত্রফল 616 বর্গমিটার এবং উচ্চতা 21 মিটার সমগ্রতলের ক্ষেত্রফল নির্ণয় কর ।
15. যে কোনো দুটি প্রশ্নের উত্তর দাও: (4×2=8)
(i) নীচের তথ্যের মধ্যমা 32 হলে, xও y এর মান নির্ণয় কর যখন পরিসংখ্যার সমষ্টি 100.
শ্রেণি সীমানা 0-10 10-20 20-30 30-40 40-50 50-60
পরিসংখ্যা 10 x 25 30 y 10
(ii) নীচের পরিসংখ্যা বিভাজনের সংখ্যাগুরুমান নির্ণয় করঃ
শ্রেণি সীমানা 0-5 5-10 10-15 15-20 20-25 25-30 30-35
পরিসংখ্যা 5 12 18 28 17 12 8
(iii) নীচের তথ্যের ক্রমযৌগিক পরিসংখ্যা (বৃহত্তর সূচক) তালিকা তৈরি করে ছক কাগজে ওজাইভ অঙ্কন করো ।
শ্রেণি সীমানা 0-5 5-10 10-15 15-20 20-25 25-30
পরিসংখ্যা 4 10 15 8 3 5
Madhyamik 2017 Mathematics Question Paper Download Links:
| Madhyamik 2017 Mathematics Question Paper Download Link | Click Here |
| Madhyamik Mathematics Question Pattern and Syllabus | Click Here |
Previous Years Madhyamik Mathematics Question Paper:
| Madhyamik Mathematics Question Paper 2024 | Click Here |
| Madhyamik Mathematics Question Paper 2023 | Click Here |
| Madhyamik Mathematics Question Paper 2022 | Click Here |
| Madhyamik Mathematics Question Paper 2020 | Click Here |
| Madhyamik Mathematics Question Paper 2019 | Click Here |
| Madhyamik Mathematics Question Paper 2018 | Click Here |
| Madhyamik Mathematics Question Paper 2017 | Click Here |