Madhyamik 2024 Mathematics Question Paper
2024
MATHEMATICS
Time — 3 Hours 15 Minutes
Full Marks {90 – For Regular Candidates, 100 For External Candidate}
1. নিম্নলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তরটি নির্বাচন করো: (1×6= 6)
i) সরল সুদ ও চক্রবৃদ্ধি সুদের হার বার্ষিক 10% হলে, দ্বিতীয় বছরে কোনো মূলধনের সরল সুদ ও চক্রবৃদ্ধি সুদের অনুপাত –
(a) 20:21
(b) 10:11
(c) 5:6
(d) 1:1
ii) যদি ax² + abcx + bc=0 (a≠0) দ্বিঘাত সমীকরণের একটি বীজ অপর বীজের অনোন্যক হয় তাহলে –
(a) abc= 1
(b) ba=c
(c) bc=1
(d) a =bc
iii) 5 সেমি ও 7 সেমি ব্যাস বিশিষ্ট দুটি বৃত্ত পরস্পরকে অন্ত:স্থভাবে স্পর্শ করলে তাদের কেন্দ্রদ্বয়ের দূরত্ব –
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4 cm
iv) tanθ + cotθ এর সর্বনিম্নমান –
(a) 0
(b) 2
(c) -2
(d) 1
v) সমান ভূমি বিশিষ্ঠ একটি নিরেট অর্ধগোলক ও একটি নিরেট চোঙের উচ্চতা সমান হলে তাদের ঘনফলের অনুপাত –
(a) 1:3
(b) 1:2
(c) 2:3
(d) 3:4
vi) প্রথম দশটি স্বভাবিক সংখ্যার গড় A এবং মধ্যমা M হলে সম্পর্কটি –
(a) A>M
(b) A< M
(c) A= 1/M
(d) A= M
2. শূন্যস্থান পূরণ করো (যে কোনো পাঁচটি): (1×5=5)
i) P এর মান কত হলে (P-3) x²+5x+ 10-0 সমীকরণটি দ্বিঘাত সমীকরণ হবে না। P = _____ ।
Ans:- 3
ii) আসল বা মূলধন এবং কোনো নির্দিষ্ট সময়ের চক্রবৃদ্ধি সুদের সমষ্টিকে_____ বলে।
Ans:- সমূল চক্রবৃদ্ধি
ii) দুটি সদৃশ ত্রিভুজের অনুরূপ বাহুগুলি_____।
Ans:- সমানুপাতি
iv) sin (0-30°) = 1/2 হলে cox এর মান হবে _____।
Ans:- 1/2
v) লম্ববৃত্তাকার শঙ্কুর আয়তন V ভূমির ব্যাসার্ধ R এবং উচ্চতা H হলে, H =______ ।
Ans:- 3v/πr²
vi) ঊর্ধ্ব ক্রমানুসারে সাজনো 8, 9, 12, 17, x+2, x+4, 30, 34, ও তথ্যের মধ্যমা 24 হলে -এর মান –
Ans:- 22
3. সত্য বা মিথ্যা লেখো (যে কোন পাঁচটি): (1×5=5)
i) অংশীদারি কারবারে তিনজন সদস্যের মূলধনের অনুপাতে a:b:c এবং নিয়োজিত সময়ের অনুপাত x:y:z হলে তাদের লাভের অনুপাত হবে ax: by: cz
Ans:- সত্য।
ii) যদি a ∝ b, b ∝ 1/3* এবং c ∝ d হয় তবে a ∝ 1/d হবে।
Ans:- মিথ্যা।
iii) কোনো বৃত্তের দুটি জ্যা কেন্দ্র থেকে সমদূরবর্তী হলে তারা অবশ্যই সমান্তরাল হবে।
Ans:- সত্য।
iv) একটি ঘড়ির ঘন্টার কাঁটা 2 ঘন্টায় π/6 রেডিয়ান কোণ আবর্তন করে।
Ans:- মিথ্যা।
V) একই ব্যাসার্ধ বিশিষ্ঠ নিরেট গোলক ও নিরেট অর্ধগোলকের সমগ্রতলের অনুপাত 2: 1
Ans:- মিথ্যা।
vi) একটি শ্রেণীতে সংখ্যক সংখ্যার গড় x̄। যদি প্রথম (n-1) সংখ্যার সমষ্টি K হয়, তাহলে n –তম সংখ্যাটি হবে (n-1) x̄+ K।
Ans:- মিথ্যা।
4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাও (যে কোনো 10 টি): (2×10=20)
i) 500 টাকার বার্ষিক 10% চক্রবৃদ্ধি সুদের হারে কত বছরের সুদ 105 টাকা হয়, নির্ণয় কর।
Ans:- 2%
ⅱ) একটি অংশীদারি কারবারে ইলা, রহিমা ও বেলার মূলধণের অনুপাত 3:8:5। ইলার লাভ বেলার লাভের চেয়ে 600 টাকা কম হলে, ব্যবসায় মোট কত টাকা লাভ হয়েছিল?
Ans:- 4800
ii) x²-22x+105= 0 সমীকরণের বীজদ্বয় ‘α’. ẞ হলে 1/α + 1/ẞ এর মান নির্ণয় করো।
Ans:- 22/105
iv) যদি (3x-2y): (3x+2y) – 4:5 হয়, তবে (x+y): (x-y) এর মান কত?
Ans:- 7:5
V) ‘O’ কেন্দ্রীয় বৃত্তে BOC ব্যাস, ABCD বৃত্তস্থ চর্তুভুজ, ∠ADC= 110° হলে ∠ACB এর মান নির্ণয় করো।
Ans:- 20°
vi) ABCD ট্রপিজিয়ামের BC || AD এবং AD = 4 সেমি, AC ও BD কর্ণদ্বয় এমনভাবে ০ বিন্দুতে ছেদ করে যে, AO/OC = DO/OB = 1/2 হয়, তাহলে BC এর দৈর্ঘ্য কত?
Ans:- 8 cm
vii) △ABC এর ∠ABC = 90°, AB-6 সেমি, BC=৪ সেমি হলে △ ABC এর পরিব্যাসার্ধের দৈর্ঘ্য কত?
Ans:- 5 cm
viii) r cos 0° = 2 √3, r sin 0°= 2 এবং 0°<0<90° হয় তাহলে r এর 0° মান নির্ণয় করো।
Ans:- 4° and 30°
ix) sin (A+B) = 1 এবং cos (A- B)= 1 হলে cot2A এর মান নির্ণয় করো।
0° ≤ (A+B) ≤90° এবং A ≥ B
Ans:- 0
x) একটি গোলকের ব্যাসার্ধের দৈর্ঘ্য দ্বিগুণ করলে বক্রতলের ক্ষেত্রফল শতকরা কত বৃদ্ধি পাবে?
Ans:- 300
xi) একটি ঘনকের প্রতিটি তলের কর্ণের দৈর্ঘ্য 6√2 সেমি হলে, ঘনকটির সমগ্র তলের ক্ষেত্রফল কত?
Ans:- 216
xii) একটি পরিসংখ্যা বিভাজনের গড় 7, ∑,fixi= 140 হলে ∑,fiএর মান নির্ণয় করো।
Ans:- 20
5. যে কোনো একটি প্রশ্নের উত্তর দাও: (5×1=5)
i) কর্মক্ষেত্র থেকে গোবিন্দবাবু কর্মক্ষেত্র থেকে অবসর নেওয়ার সময় 5,00,000 টাকা পেলেন। ঐ টাকার কিছুটা ব্যাঙ্ক ও বাকিটা পোস্ট অফিসে জমা রাখেন। প্রতি বছর সুদ বাবদ 33,600 টাকা পান। ব্যাঙ্ক ও পোস্ট অফিসে বার্ষিক সরল সুদের হার যথাক্রমে 6% ও 2%। তিনি কোথায় কত টাকা রেখেছিলেন তা নির্ণয় করো।
ii) আমন 25,000 টাকা 3 বছরের জন্য এমনভাবে ধার করলেন যে, প্রথম, দ্বিতীয় ও তৃত্বীয় বছরে বার্ষিক চক্রবৃদ্ধি সুদের হার যথাক্রমে 4%, 5% ও 6%, 3 বছরের শেষে আমন সুদে আসলে কত টাকা জমা দেবে?
6. যে কোনো একটি প্রশ্নের উত্তর দাও:
i) A এর গতিবেগ B এর গতিবেগের থেকে 1 মিটার/সেকেণ্ড বেশী। 180 মিটার দৌড়াতে গিয়ে A, B এর থেকে 2 সেকেণ্ড আগে পৌঁছায়। B-এর গতিবেগ প্রতি সেকেণ্ডে কত মিটার? 3
ii) সমাধান করো:
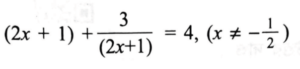
7. যে কোনো একটি প্রশ্নের উত্তর দাও:

8. যে কোনো একটি প্রশ্নের উত্তর দাও:

9. যে কোনো একটি প্রশ্নের উত্তর দাও: 5
i) একই বৃত্তাংশস্থ সকল কোণের মান সমণ-প্রমাণ করো।
ii) প্রমাণ করো যে, বৃত্তের বহিস্থ কোন বিন্দু থেকে যে দুটি স্পর্শক অঙ্কন করা যায় তাদের স্পর্শবিন্দু দুটির সঙ্গে বহিস্থ বিন্দুর সংযোজক সরলরেখাংশ দুটির দৈর্ঘ্য সমান এবং তারা কেন্দ্রে সমান কোণ উৎপন্ন করে।
10. যে কোনো একটি প্রশ্নের উত্তর দাও: 3
i) O কেন্দ্রীয় বৃত্তের পরিলিখিত চতুর্ভুজ ABCD হলে প্রমাণ করো যে, AB + CD = AD + BC |
ii) PQR সমকোণী ত্রিভুজের ∠P =90° এবং PS, অতিভুজ QR-এর ওপর লম্ব। প্রমাণ করো যে
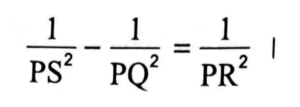
11. যে কোনো একটি প্রশ্নের উত্তর দাও:
i) 4 সেমি ব্যাসার্ধ বিশিষ্ট একটি বৃত্ত অঙ্কন করো। ওই বৃত্তের কেন্দ্র থেকে 9 সেমি দূরত্বে একটি বিন্দু থেকে বৃত্তের উপর একটি স্পর্শক অঙ্কন করো।
ii) একটি সমকোণী ত্রিভুজ অঙ্কন করো যার সমকোণ সংলগ্ন বাহুদ্বয় 4 সেমি এবং 5 সেমি। ঐ ত্রিভুজটির একটি পরিবৃত্ত অঙ্কন করো ।
12. যে কোনো দুইটি প্রশ্নের উত্তর দাও: (3×2=6)
i) কোন সমকোণী ত্রিভুজের দুটি সূক্ষ্ম কোণের অন্তর 72° হলে কোণ দুটির বৃত্তীয়মান নির্ণয় করো।

13. যে কোনো একটি প্রশ্নের উত্তর দাও:
i) কোন স্তম্ভের একই পার্শ্বে এবং পাদবিন্দুগামী একই অনুভুমিক সরলরেখায় অবস্থিত দুটি বিন্দু থেকে স্তম্ভের শীর্ষের উন্নতি কোণ যথাক্রমে 0 এবং ɸ। স্তম্ভের উচ্চতা h হলে বিন্দু দুটির দূরত্ব নির্ণয় করো।
ii) 120 মিটার চওড়া রাস্তার দুপাশে ঠিক বিপরীতে A ও B বিন্দুতে দুটি সমান উচ্চতার স্তম্ভ আছে। স্তম্ভ দুটির পাদবিন্দুর সংযোগ রেখার উপর C বিন্দু থেকে A ও B বিন্দুতে স্তম্ভ দুটির শীর্ষের উন্নতি কোণ যথাক্রমে 60° ও 30° হলে AC মান নির্ণয করো।
14. যে কোনো দুইটি প্রশ্নের উত্তর দাও: (4×2=8)
i) একটি আইসক্রীমের নিচের অংশ শঙ্কু আকৃতি ও ওপরের অংশ অর্ধগোলাকৃতি যাহাদের ভূমি একই। শঙ্কুর উচ্চতা 9 cm এবং ভূমির ব্যাসার্ধ 5 cm হলে, আইসক্রীমটির আয়তন নির্ণয় করো।
ii) একটি ফাঁপা চোঙাকৃতি পাইপের বাইরের ও ভিতরের বক্রতলের ক্ষেত্রফলের অন্তর 44 বর্গ সেমি এবং পাইপের দৈর্ঘ্য 14 সেমি, পাইপটির পদার্থের ঘনফল 99 ঘন সেমি। পাইপটির বাইরের ও ভেতরের ব্যাসার্ধ নির্ণয় করো।
iii) ঘনকাকৃতির একটি সম্পূর্ণ জলপূর্ণ চৌবাচ্চা থেকে সমান মাপের 75 বালতি জল তুলে নিলে চৌবাচ্চাটির অংশ জলপূর্ণ থাকে। চৌবাচ্চাটির একটি ধারের দৈর্ঘ্য 1.5 মিটার হলে প্রতি বালতিতে কত লিটার জল ধরে?
15. যে কোনো দুইটি প্রশ্নের উত্তর দাও: (4×2=8)
i) নীচের তথ্যের সংখ্যাগুরু মান নির্ণয় করো।
| শ্রেনী | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 | 30-35 | 35-40 |
| পরিসংখ্যা | 2 | 6 | 10 | 16 | 22 | 11 | 8 | 5 |
ii) নিম্নলিখিত পরিসংখ্যা বিভাজন ছক থেকে যে কোনো পদ্ধতি গড় নির্ণয় করো।
| শ্রেনী সীমা | 85-105 | 105-125 | 125-145 | 145-165 | 165-185 | 185-205 |
| পরিসংখ্যা | 3 | 12 | 18 | 10 | 5 | 2 |
iii) নীচের পরিসংখ্যা বিভাজন থেকে তথ্যটি মধ্যমা নির্ণয় করো।
| প্রাপ্ত নম্বর | 5-এর কম | 20-এর কম | 30-এর কম | 40-এর কম | 50-এর কম | 60-এর কম |
| পরিসংখ্যা | 8 | 15 | 29 | 42 | 60 | 70 |
Madhyamik 2024 Mathematics Question Paper | Madhyamik Mathematics Question Paper 2024 | Madhyamik Mathematics 2024 Question Paper with Answer | Madhyamik 2024 Mathematics Solved Question Paper | Madhyamik Mathematics Question Paper 2024 PDF Download | WBBSE Class 10 Mathematics Question Paper 2024 | মাধ্যমিক অঙ্ক প্রশ্নপত্র ২০২৪ | মাধ্যমিক ২০২৪ অঙ্ক প্রশ্নপত্র এবং উত্তর | মাধ্যমিক ২০২৪ অঙ্ক প্রশ্নপত্র Download করুন উত্তর সহ | মাধ্যমিক ২০২৪ অঙ্ক প্রশ্নপত্র উত্তর সহ (PDF)
Previous Years Madhyamik Mathematics Question Paper:
| Madhyamik Mathematics Question Paper 2024 | Click Here |
| Madhyamik Mathematics Question Paper 2023 | Click Here |
| Madhyamik Mathematics Question Paper 2022 | Click Here |
| Madhyamik Mathematics Question Paper 2020 | Click Here |
| Madhyamik Mathematics Question Paper 2019 | Click Here |
| Madhyamik Mathematics Question Paper 2018 | Click Here |
| Madhyamik Mathematics Question Paper 2017 | Click Here |